Transformer打破三十年数学猜想,Meta研究者用AI给出反例,算法杀手攻克数学难题!
Transformer打破三十年数学猜想,Meta研究者用AI给出反例,算法杀手攻克数学难题
一种名为PatternBoost的新方法在数学问题中寻找有趣的结构,这种方法结合了局部搜索和全局搜索。其核心思想是交替进行这两个阶段:首先使用传统算法生成许多理想的构造,然后利用Transformer神经网络对这些构造进行训练,再将训练好的模型用作下一个阶段的种子,并重复此过程。

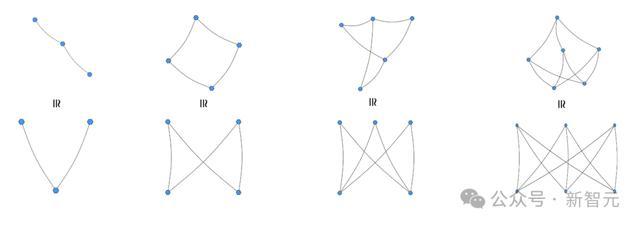
这种方法在多个数学领域进行了测试,尤其在解决一些长期未解的问题上表现出色。例如,它不仅找到了某些问题的最佳已知解决方案,还反驳了一个悬而未决30年的猜想。一个具体的例子是在无4-圈问题上的应用,即在给定顶点数的情况下,构造尽可能多的边而不包含4个顶点组成的闭合路径。PatternBoost通过多轮迭代在这个问题上取得了比传统方法更好的结果。
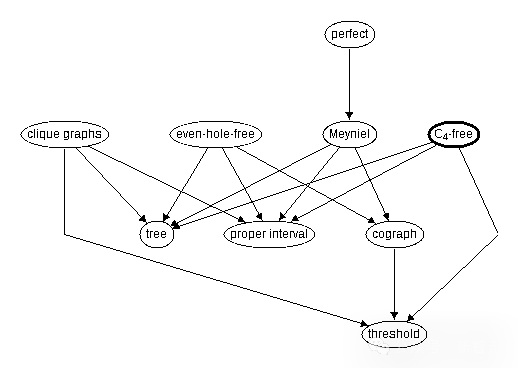
另一个应用案例是关于图中没有三角形的最大边数问题。研究者发现,许多表现最优的图形都是二分图,这符合Turán三角定理或Mantel定理。然而,当问题变得更加复杂时,如涉及五边形等更复杂的结构时,研究者很难仅凭直觉找到规律。PatternBoost提供了一种通用的方法来逼近这些结构。具体步骤包括确定局部搜索方法和评分函数,创建起始数据库,训练Transformer,从Transformer获取新结构,运行本地搜索,以及重复这一过程。
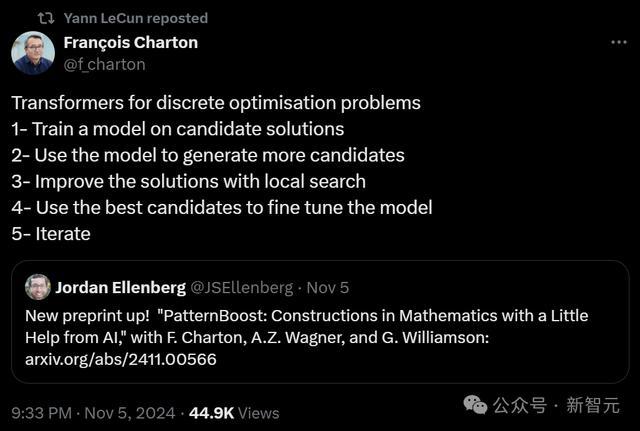
此外,PatternBoost还在d-维超立方体直径为d的生成子图问题上取得突破。该问题最早由Niali Graham和Frank Harary提出,即在不增加其直径的情况下,可以从d-维超立方体中删除的最大边数是多少?研究者通过PatternBoost找到了一个反例,推翻了之前的猜想,这是30年来首次在这个问题上取得进展。
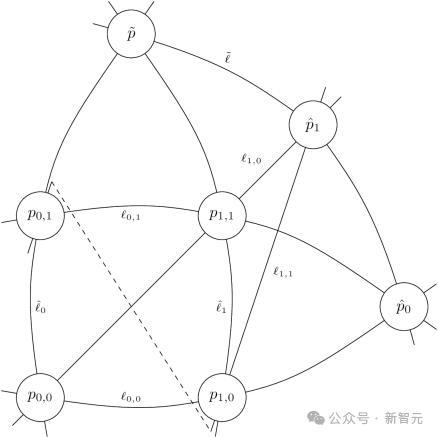
PatternBoost展示了机器学习技术在数学中的潜力。通过结合局部和全局搜索,它能够在多种数学问题中生成有趣的构造,并且具有广泛的应用前景。这种方法不仅提高了优化问题的解决方案,还为数学工作者提供了一个简单易用的工具。
免责声明:本文章由会员“极目新闻”发布如果文章侵权,请联系我们处理,本站仅提供信息存储空间服务如因作品内容、版权和其他问题请于本站联系
